I quadrilateri
Abbiamo ripassato le proprietà dei quadrilateri.
Ho fatto visionare un video che secondo me è fatto molto bene. I bimbi man mano hanno disegnato.
Le proprietà dei quadrilateri le ho fatte sin dalla terza con il diagramma di Venn classico sui quadrilateri che trovi su internet…
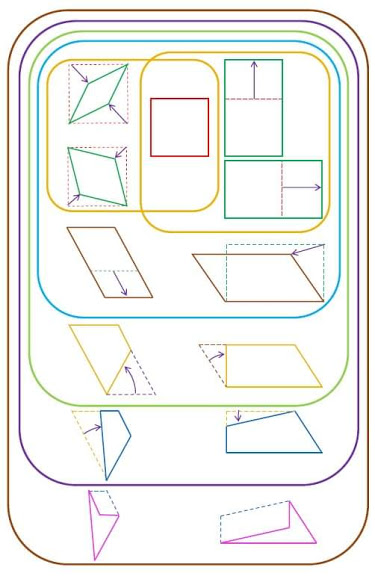
Quest’anno sto utilizzando un diagramma diverso dal solito realizzato da Giovanni Castiglioni … Un diagramma che si basa sulla “proprietà di sottrazione”… come ha scritto l’autore stesso.
Lo schema è chiaro, si parte dal quadrato per poi sottrarre le proprietà ai vari quadrilateri.
Le definizioni che ho dato io sono le seguenti, prese dal sito di Geometriko… consigliato in un post da Antonella Castellini.
Definizione (Quadrilatero Scaleno).
Si definisce quadrilatero scaleno un quadrilatero che non ha né angoli e né lati congruenti.
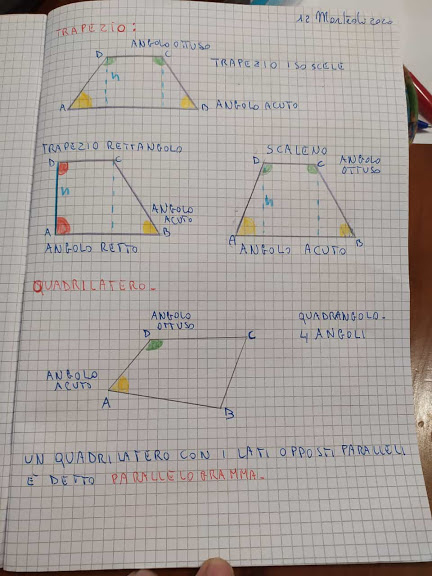
Definizione (Trapezio)
Si definisce trapezio un quadrilatero che ha (almeno) una coppia di lati paralleli.
Dato un trapezio, si definiscono:
– Basi del Trapezio i lati paralleli del trapezio;
– Lati del Trapezio, gli altri due lati (su altri testi sono denominati Lati Obliqui).
Definizione (Trapezio Rettangolo)
Si definisce Trapezio Rettangolo un trapezio con due lati perpendicolari.
Definizione (Trapezio Isoscele)
Si definisce trapezio isoscele un trapezio in cui i due lati (ex lati obliqui) sono congruenti e gli angoli adiacenti ad almeno una delle basi sono congruenti.
Definizione (Trapezio Scaleno)
Si definisce Trapezio Scaleno un trapezio non isoscele.
Definizione (Parallelogramma)
Si definisce Parallelogramma un qualunque quadrilatero avente i lati opposti paralleli.
Definizione (Deltoide)
Si definisce deltoide un qualunque quadrilatero avente i lati consecutivi a due a due congruenti.
Definizione (Romboide)
Si definisce romboide un parallelogramma privo di congruenze tra lati consecutivi o angoli adiacenti.
Definizione (Rettangolo)
Si definisce rettangolo un qualunque quadrilatero che ha tutti gli angoli congruenti.
Definizione (Rombo o Losanga)
Si definisce rombo o losanga un qualunque quadrilatero che ha tutti i lati congruenti.
Definizione (Quadrato)
Si definisce quadrato un qualunque quadrilatero che ha tutti gli angoli e i lati congruenti.
INSIEME QUADRILATERI AVANZATO (by Leonardo Tortorelli)
(Docenti Scuola Media e Superiore/Liceo Scientifico ed eccellenze di altri indirizzi)
Di solito con lo schema davanti faccio domande specifiche sui quadrilateri ai bimbi… alle quali devono rispondere Si’ NO, perché…
Ad esempio
Il quadrato è un trapezio? Sì, perché? … perché ha almeno una coppia di lati paralleli.
Il trapezio è un parallelogramma? No, perché? Perché non ha tutti i lati opposti paralleli ecc…
Quindi con il diagramma è più semplice… I diagrammi sono tratti sempre dal sito Geometriko
Il quadrilatero è una figura piana delimitata da 4 lati. Possono essere concavi o convessi.
Quadrilateri convessi
Il Deltoide è un qualunque quadrilatero avente i lati consecutivi a due a due congruenti (l’aquilone dico ai bimbi)
Il Trapezio è un quadrilatero che ha (almeno) una coppia di lati paralleli.
I prossimi quadrilateri descritti sono tutti TRAPEZI
Il Parallelogramma è un qualunque quadrilatero avente i lati opposti paralleli.
I prossimi quadrilateri descritti sono tutti PARALLELOGRAMMI
Il Romboide è un parallelogramma privo di congruenze tra lati consecutivi o angoli adiacenti.
Il romboide è un quadrilatero, è un trapezio, è un parallelogramma.
Il Rettangolo è un qualunque quadrilatero che ha tutti gli angoli congruenti.
Il rettangolo è un quadrilatero, è un trapezio, è un parallelogramma.
Il Rombo o Losanga è un qualunque quadrilatero che ha tutti i lati congruenti.
Il rombo è un quadrilatero, è un trapezio, è un parallelogramma.
Il Quadrato è un qualunque quadrilatero che ha tutti gli angoli e i lati congruenti.
Il quadrato è un quadrilatero, un trapezio, un parallelogramma, un rettangolo, un rombo.


Potrebbero anche interessarti…
GIOCHI DI MATEMATICA Archivi Maestra Anita
(Tra i giochi, ne trovi tanti sulle frazioni. Il link è condivisibile con gli alunni)
Quaderno di GEOMETRIA dalla Prima alla Quinta
Laboratorio di matematica Maestra Anita
Se ti interessano delle bellissime attività di laboratorio ti consiglio questi siti…
ll materiale presente sul sito Maestra Anita è di proprietà esclusiva di Maestra Anita. Puoi condividere, in altri siti o sui social, i link dei vari articoli presenti sul sito che rimandano al blog Maestra Anita. Puoi scaricare i file e utilizzarli con i bambini, puoi condividere i file tramite registro elettronico. È vietata la pubblicazione delle foto delle pagine dei quaderni, dei singoli file word, file pdf, file di presentazioni in power point in altri siti, o sui social, senza preventiva autorizzazione.